[당주힘실 통계학] 11-2. 정규모집단 추론_분산(퍼진 정도), 카이제곱 분포

당.주.힘.실 : 당신의 주장에 힘을 실어줄

 

 

---

모평균처럼 모집단의 중심위치뿐 아니라 모집단의 퍼져 있는 정도가 관심의 대상이 될 수도 있다. 이것은 모집단의 중심위치가 얼마나 안정적으로 유지하는가에 대한 의미이다. 이 퍼진 정도는 표준편차에 대한 추론이 필요하다. 모표준편차의 대한 추론은 반드시 정규분포를 따른다는 전제를 갖는다. t 분포에서의 모표준편차 추론은 모평균의 추론보다 훨씬 심각한 오류를 범할 가능성이 있다. 따라서 모집단의 정규성 여부 판단이 최우선이다.

 

모표준편차에 대한 추론

모표준편차는 모분산에 대한 추론으로부터 시작한다. 모분산 추론을 위한 통계량으로 표본분산은 아래와 같다.

표본분산

 

점추정의 경우 σ^2의 추정량으로 s^2을 사용하고 모표준편차의 추정량으로 표본표준편차 s를 사용한다. 구간추정이나 검정의 경우에는 s^2의 분포가 필요한데, 그 분포는 x^2 분포(chi-square distribution)와 연관 있다.

 

1. x^2 분포, chi-square distribution

정규모집단 N(μ, σ^2)으로부터 추출된 표본을 X1,..., Xn이라고 할 때 x^2은 자유도가 n-1인 x^2 분포를 따른다고 하고, 이를 기호로써 x^2(n-1)로 표현한다.

 

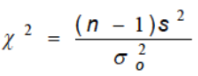
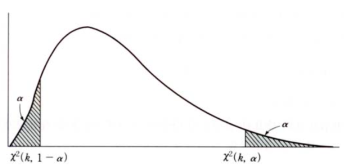
x^2 분포는 정규분포나 t 분포와는 달리 확률밀도함수가 양수 쪽에만 퍼져 있고 오른쪽에 긴 꼬리를 갖는 비대칭형이다. 또한 자유도에 따라 분포가 달라지는데 자유도가 클수록 0으로부터 멀리 떨어져서 넓게 분포한다.

x^2 분포그래프 (k : 자유도)

 

x^2 분포표에는 추론에서 자주 쓰이는 몇 개의 a 값과 자유도 r(=d.f.)에 대해 x^2 분포의 상위 a의 확률을 주는 값이 주어져 있다. 이 값을 (x_a)^2(r)로 표현하면 자유도 r인 확률변수 x^2에 대하여 P[x^2>= (x_a)^2(r)]= a를 만족시킨다. 한편 하위 a의 확률을 주는 값은 (x_1-a)^2(r)로 구할 수 있다.

t 분포표 (d.f. = degree of freedom)

 

2. 모표준편차의 신뢰구간

표본분산 s^2을 이용하여 σ^2의 신뢰구간을 구한다. σ^2의 신뢰구간은 s^2의 분포로부터 얻어지는데, 이 분포로부터 구한 신뢰구간은 이제까지 구한 신뢰구간들과는 형태가 다르다. (종 모양이 아닌 오른쪽에 긴 꼬리를 갖기 때문이다.)

(n-1)s^2/σ^2 ~ x^2(n-1)

카이분포표 상하위 a의 확률, 신뢰구간 구하는 방식에 차이는 없다

 

그러나 이제까지 신뢰구간을 구하는 방식에는 차이가 없다. 마찬가지로 a라는 확률을 x^2 분포의 양 끝으로 똑같이 a/2씩 나누어 준 값들을 이용하게 된다. 이때 σ^2의 100(1-a)% 신뢰구간을 구한다. σ의 신뢰구간은 σ^2 신뢰구간의 제곱근이다.

카이제곱 분포에 따라 구간별 고려가 출발이다

 

정규 모집단 σ^2의 100(1-a)% 신뢰구간

 

여기서 한 가지 주의할 점은 σ의 경우 신뢰구간의 중심이 그 추정치인 s가 아니라는 것이다. 모평균, 모비율과의 가장 큰 차이점이다.

 

3. 검정 추론

표준편차에 대한 검정이나 분산에 대한 검정의 과정이 완전히 일치하다. 왜냐하면 가설 H0의 σ=σ0와 σ^2=σ0^2은 같기 때문이다. 아래 정리로 이번 장을 마무리한다.

 

< 모표준분산 σ^2에 대한 추론 (정규모집단일 때) >

- 자료 : 표준분산이 σ^2 인 정규모집단으로부터 추출한 X1, ...,Xn

- σ^2의 추정량 : s^2

표본분산

 

- σ^2에 대한 100(1-a)% 신뢰구간

정규 모집단 &sigma;^2의 100(1-a)% 신뢰구간

 

- 정규모집단의 모표준분산 σ^2에 대한 가설 H0 : σ^2= σ0^2를 검정하기 위한 검정통계량은 다음과 같다.

x^2 = (n-1) / (s/σ)^2

 

(각 대립가설에 대한 기각역)

H1 : σ^2< σ0^2, R : x^2>= (x_a)^2(n-1)

H1 : σ^2> σ0^2, R : x^2<= (x_1-a)^2(n-1)

H1 : σ^2≠ σ0^2, R : x^2>= (x_a/2)^2(n-1) or x^2<= (x_1-a/2)^2(n-1)

 

한 줄 요약
중심축을 얼마나 유지하는지는 퍼진 정도에 대한 불확실성에 대한 검증이 필요하다. 그것은 카이제곱 분포를 통해 알 수 있다.

 

---