
당.주.힘.실 : 당신의 주장에 힘을 실어줄
두 모집단 간의 차이가 관심의 대상이 된다. 예를 들면 기존의 것과 변경점을 갖는 것의 효과 비교와 같은 것이다. 두 모집단의 비교를 위한 추론 가정은 자료를 어떻게 수집하느냐에 따라 추론 방법이 달라진다. 두 종류의 자료수집 과정에 따른 추론 방법을 소개한다. 그전에 기본적인 용어를 정의한다.
- 처리 : 비교하고자하는 특성, 일종의 개별적 모집단이 될 수 있다.
- 실험단위 : 실험 대상
- 반응값 : 실험 후에 얻어지는 수치
1. 두 개의 독립표본 비교 : 임의로 두 그룹으로 나누어 한 그룹에는 처리1, 다른 그룹에는 처리2를 배정. 각 그룹의 실험대상으로부터 얻어지는 반응 값들은 서로 영향을 주지 않는 독립이다. 예를 들어 조건이 비슷한 총 20개의 표본 중 10개씩 나누어 처리1, 처리2를 배정하는 것이므로 시행하는 데 있어 두 그룹 간 독립됨을 의미한다.
2. 짝비교 : 실험대상들의 외적인 조건이 많아서 최대한 비슷한 조건의 실험대상끼리 짝을 짓는다. 그리고 각 쌍에 있는 하나는 처리1, 나머지는 처리2를 배정한다. 이때 짝 지우는 과정에 각 쌍에 있는 실험단위들은 비슷한 특성을 갖게 되므로 서로 독립이라 할 수 없다. 이 경우 각 쌍마다 한 쌍의 반응값을 관측하여 서로 비교하게 된다.
개념을 좀 더 명확히 하기 위해 다음 소개될 내용들을 알아보고 간단한 이해를 위한 최종 정리를 할 예정이다. 추가로 두 모비율의 차이를 추론하는 방법을 정리할 것이다.
두 개의 독립 표본 (표본의 크기가 클 때)
독립인 두 개의 표본으로부터 두 모집단, 혹은 두 가지의 처리효과를 비교하는 통계추론의 방법이다. 마치 독립된 두 개의 비커에서 각각 다른 처리를 시행하고 그 반응 값을 얻는 것으로 직관적 이해가 가능하다. 두 모집단으로부터 추출된 표본과 그로부터 계산되는 통계량을 정리한 것이다.
1. 최초 설정
- 모집단 : X & Y, 표본 : X1, ...,Xn & Y1,..., Yn
- 평균 : μ1 & μ2, 표준편차 : σ1 & σ2
- 표본평균

- 표본분산

여기서 우리의 관심사는 두 모집단의 평균 반응 값의 차이다. 즉 μ1 - μ2에 대한 추론이 필요하다.
2. 모평균의 차에 대한 추론 (표본의 크기가 클 때)
두 모평균의 차에 대한 추론은 두 표본평균의 차를 이용한다. 두 표본의 크기가 모두 30이상으로 큰 경우 중심극한정리에 의해 표본평균은 다음과 같이 근사적으로 정규분포를 따른다.

정리하면, 두 개의 확률변수 X, Y가 서로 독립이고 다음과 같이 정규분포를 따를 때 두 변수의 합과 차는 각각 정규분포를 따른다.


두 표본은 서로 독립이므로 두 표본평균의 차 역시 정규분포를 따른다. 따라서 표준화된 확률변수는 표준정규분포를 따르고, 모분산을 모를 때에는 이를 표본분산으로 대체하여도 다음과 같이 근사적으로 표준정규분포를 따른다.


이 분포를 바탕으로 μ1 - μ2에 대한 100*(1-a)% 신뢰구간은 다음의 형식에 따라 최종 정리가 가능하다.


3. H0 : μ1-μ2 = δ0에 대한 검정 (표본의 크기가 클 때)
표본의 크기 n1, n2가 모두 30 이상일 때 가설 H0에 대한 검정 통계량은 다음과 같다.
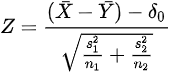
검정통계량의 분포는 H0이 맞을 때 N(0, 1)을 따른다. 각 대립가설에 대하여 유의수준 a를 갖는 기각역은 다음과 같다.
H1 :μ1-μ2 < δ0, R : Z<= -z_a
H1 : μ1-μ2 > δ0, R : Z>= z_a
H1 : μ1-μ2 ≠ δ0, R : |Z|>= z_a/2
두 개의 독립 표본 (표본의 크기가 작을 때)
표본의 크기가 작을 때에도 결국 두 모집단에 대하여 정규분포 가정이 필요하다. 또한 두 모집단의 표준편차에 대한 가정이 필요한데, 그 하나는 두 모집단의 표준편차가 같다고 가정하는 경우이고 하나는 다르다고 가정하는 경우다. 두 모집단의 표준편차 동일 여부의 기준은 표본의 표준편차를 이용한다. 두 표본 표준편차의 비율 s1/s2가 1에 가까우면 모표준편차가 동일하다는 가정이 적합할 수 있다.
1. 표본의 크기가 작을 때 필요한 가정
(1) 두 모집단이 모두 정규분포를 따른다.
(2) 두 모집단의 표준편차가 일치한다. (σ1=σ2=σ)
* 일치하지 않을 때 판단 기준은 이 페이지 가장 하단을 참조
두 모집단의 공통 표준편차인 σ를 아는 경우에는 정규분포를 이용하여 추론할 수 있으나 대부분의 경우 σ를 모르므로 별도의 σ 추정이 필요하다. σ에 대한 정보는 각 표본의 편차 제곱합에 포함되어 있다. 이 두 제곱합을 더하여 각각의 자유도의 합을 나누어 분산 σ^2의 추정량으로 사용한다. 이를 공통 분산의 합동 추정량이라고 한다.

2. 모평균의 차에 대한 추론 (표본의 크기가 작을 때)
두 정규모집단에서 독립적으로 추출된 두 표본으로부터 얻게 되는 표준화된 확률변수는 자유도가 n1+n2-2 인 t 분포를 따른다.

이 분포를 바탕으로 μ1 - μ2에 대한 100*(1-a)% 신뢰구간은 다음의 형식에 따라 최종 정리가 가능하다.


3. H0 : μ1-μ2 = δ0 에 대한 검정 (표본의 크기가 작을 때)
표본의 크기가 작고 모표준편차가 같을 때 가설 H0에 대한 검정 통계량은 다음과 같다.
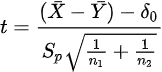
검정통계량의 분포는 H0이 맞을 때 자유도가 (n1+n2-2)인 t분포를 따른다. 각 대립가설에 대하여 유의수준 a를 갖는 기각역은 다음과 같다.
H1 :μ1-μ2 < δ0, R : t<= -t_a(n1+n2-2)
H1 : μ1-μ2 > δ0, R : t>= t_a(n1+n2-2)
H1 : μ1-μ2 ≠ δ0, R : |t|>= t_a/2(n1+n2-2)
* 두 모집단의 표준편차가 같지 않을 때
표본의 크기가 클 때 사용하였던 표준화된 확률변수는 표본의 크기가 작고 두 모표준편차가 같지 않을 경우에 근사적으로 t 분포를 따른다. 이때 자유도는 (n1-1), (n2-1) 중 작은 값이다.
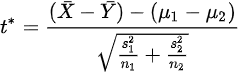
1.
이 분포를 이용한 모평균의 차의 100(1-a)% 신뢰구간은 근사적으로 아래와 같다. 이때 t*의 자유도는 n1-1, n2-1 중 작은 값이다.
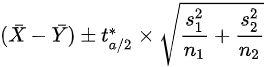
2.
가설 H0 : μ1-μ2= δ0에 대한 검정 통계량은 다음과 같다. 이 검정통계량의 분포는 H0이 맞을 때 근사적으로 자유도가 n1-1, n2-1 중 작은 값인 t 분포를 따른다.

여기서 제시하는 방법은 조금 보수적인 성질을 갖는다. 즉 신뢰구간의 경우 그 구간이 넓어지는 경향이 있다. 따라서 실제 신뢰도가 100(1-a)% 이상이 된다. 검정의 경우 기각역이 좁아지는 경향이 있어서 실제 유의수준이 a 이하가 되므로 귀무가설을 기각하지 못할 가능성이 높다.
한 줄 요약
서로 독립인 두 모집단을 비교할 때 표본의 크기에 맞춰 특정 분포를 따른다. 그리고 모평균의 차를 통하여 신뢰구간을 확인하거나 가설검정으로 추론이 가능하다.
'@ '통계학' 당주힘실' 카테고리의 다른 글
| [당주힘실 통계학] 13. 회귀분석_여러개의 변수 (0) | 2022.08.21 |
|---|---|
| [당주힘실 통계학] 12-2. 두 모집단의 비교_짝비교, 모비율의 차이 (0) | 2022.08.20 |
| [당주힘실 통계학] 11-2. 정규모집단 추론_분산(퍼진 정도), 카이제곱 분포 (0) | 2022.08.19 |
| [당주힘실 통계학] 11-1. 정규모집단 추론, 표본의 크기가 작을 때_t 분포, 모평균 (0) | 2022.08.19 |
| [당주힘실 통계학] 10-2. 통계적 추론, 표본의 크기가 클 때_모평균의 가설 검정 (0) | 2022.08.18 |




댓글