
당.주.힘.실 : 당신의 주장에 힘을 실어줄
히스토그램은 계급구간의 폭, 시작값 등에 따라 달라지는 것처럼 그림이나 도표의 모양이 작성자의 주관적 판단에 따라 달라진다. 일관성과 객관성을 보완하기 위해 방대한 양의 자료를 몇 개의 의미 있는 수치로 요약하여 자료의 대략적인 분포상태를 파악할 수 있는 통계기법을 고려한다.
중심위치의 측도
자료에서 중심이 되는 위치값을 결정.
- 평균(Mean) : 모든 관측값의 합계 / 총 자료의 개수, 값이 하나가 너무 커지면 중심에 영향을 주는 단점이 있다. 관측값의 산술평균으로서 통계적 추론과정에서 광범위하게 사용된다. 기초적인 통계수치로 가장 많이 사용한다.
- 중앙값(Median) : 자료의 개수(n)가 1. 홀수일 경우 (n+1)/2 번째 관측값, 2. 짝수일 경우 n/2번째 관측값과 n/2 +1번째 관측값 사이의 중간값 또는 평균. 즉, 전체 관측값을 반으로 나누는 경곗값. 표본평균과는 달리 중앙값은 관측값들의 변화에 민감하지 않고 특히 아주 큰 관측값이나 아주 작은 관측값에 영향을 받지 않는다.
- 최빈값(Mode) : 최빈값은 관측값 중에서 가장 자주 나오는 값을 말한다. 이산형 자료나 범주형 자료에서 흔히 사용된다. 연속형 자료의 경우에는 도수분포표로 자료를 그룹화하여 최대의 도수를 갖는 계급구간의 중간값을 최빈값으로 정한다. 그러나 다음과 같은 이유로 잘 사용하지 않는다.
1. 도수분포표를 사용할 때 계급구간의 폭에 따라 최빈값이 달라진다.
2. 이봉형 분포를 갖는 자료에서 여러 개의 최빈값이 존재할 수 있는데, 중심 위치로서의 의미가 줄어든다.
실제 중심 위치의 측도로 사용할 때에는 표본평균 > 중앙값 순으로 사용한다. 극단적인 관측값이 있는 경우, 표본평균과 중앙값 중에서 상황에 따라 적합한 것을 사용하여야 할 것이다. 전체의 경향을 볼 때 극단적인 관측값의 영향을 배제하고 싶으면 중앙값이 바람직하고 전체 관측값을 모두 포함하고 싶으면 평균을 사용하는 것이 바람직하다.
분포가 치우친 경우 중심위치의 측도들은 서로 다른 값을 갖게 된다. 분포가 왼쪽으로 치우친 경우에는 평균이 중앙값보다 크게 되는데, 이것은 평균이 소수의 아주 큰 값들에 영향을 받기 때문이다. 또한 분포가 오른쪽으로 치우친 경우에는 평균이 중앙값보다 작게 된다. 이와 같이 분포의 모양에 따라서 표본평균과 중앙값의 위치가 정해지는데, 때때로 평균과 중앙값의 위치를 가지고 분포의 모양을 판단하기도 한다.
퍼진정도의 측도
중심위치가 같지만 분포의 퍼진 정도가 다른 경우 중심위치만을 가지고 두 분포를 설명할 수 없다. 따라서 중심의 위치에 대한 측도와 더불어 퍼진 정도를 측정하기 위한 수치가 필요하다.
- 편차 : 표본평균을 중심위치의 측도로 사용할 때 각 관측값과 평균의 차이. 관측값-표본평균. 편차의 전체 합은 항상 0이다.
- 표본분산(sample variance, s^2) : 편차의 제곱합을 구한 후에 관측값의 개수에서 1을 뺀 값으로 나눈다. 표본분산의 값이 클수록 관측값들이 표본평균으로부터 멀리 퍼져 있다는 것을 알 수 있다. 표본 표준편차(s)는 표본분산 양의 루트값이다.


- 범위 : 관측값 중에서 최댓값 - 관측값 중에서 최솟값. 퍼진 정도를 나타내는 또 다른 측도. 양 끝점에 의해서만 결정되기 때문에 중간에 위치한 관측값들이 어떻게 퍼져 있는가 하는 것이 전혀 고려되지 않는 단점이 있다.
- 백분위수 : 자료의 수가 n개일 때, 제 100*p 백분위수는 그 값보다 작거나 같은 관측값의 갯수가 np개 이상이고 그 값보다 크거나 같은 관측값이 n(1-p)개 이상인 값이다.
1. 관측값을 작은 순서로 배열한다. 그리고 관측값의 갯수(n)에 p를 곱한다.
2. np가 정수, np번째로 작은 관측값과 np+1번째로 작은 관측값의 평균을 제 100*p 백분위수로 한다.
3. np가 정수가 아닐 경우, np에서 정수부분에서 1을 더한 m값을 구한다. 그리고 m번째 작은 관측값을 제 np 백분위수로 한다.
- 사분위수 : 전체 관측값을 작은 순서로 배열하였을 때 사분위수는 전체를 사등분하는 값을 나타낸다. 전체의 사분의 1, 사분의 2, 사분의 3은 각각 전체의 25%, 50%, 75%이므로 제 1 사분위수(제 25백분위수, Q1), 제 2 사분위수(제 50백분위수, Q2, 중앙값), 제 3 사분위수(제 75백분위수, Q3)가 된다. 이때 제 3사분위수와 제 1사분위수 사이의 거리를 퍼진 정도의 측도로 사용한다. 이 수치를 사분위수범위(Interquartile range, IQR)이라 한다. 극단값에 영향을 받지 않고 한쪽으로 치우친 분포에서 극단값을 제외한 퍼진 정도를 알려고 할 때 유용하다.
표준편차는 표본평균과 같은 이론적 배경이고, 사분위수범위는 중앙값과 같은 이론적 배경을 갖는다. 따라서 예를 들면 중심위치의 측도로 표본평균을 사용할 경우 표준편차를 퍼진 정도의 측도로 쓰는 것이 바람직하다. 사분위수범위는 각 관측값의 퍼진 정도를 전체적으로 반영하지는 않지만 극단적인 관측값에 자유롭다. 범위는 극단적 관측값에 영향을 받고, 보통 관측값도 골고루 반영하지 않는 점에서 단점이 많아 사용하지는 않는다.
- 변동계수 : 예를 들어 단위가 다르거나 중심위치가 매우 다른 두 개 이상의 분포를 비교할 때 이들 수치를 가지고 퍼진 정도를 비교하는 것은 불합리하다. 이러한 경우에 상대적으로 퍼진 정도를 나타내는 수치로 사용한다. (* CV = (표준편차/표본평균) * 100 )
상자그림 (box plot)
상자그림은 자료로부터 얻는 다섯 가지의 요약수치인 최솟값,Q1, Q1, Q3, 최댓값을 가지고 그림을 그린 것이다.
<상자그림 작성과정>
1. 사분위수를 결정한다. (Q1, Q2, Q3)
2. Q1, Q3를 네모난 상자로 연결하고, Q2의 위치에 수직선을 긋는다.
3. Q3 - Q1 = IQR을 계산하고 이에 1.5를 곱한 값을 상자 양끝의 범위로 경계한다. 이 범위에 포함되는 최솟값과 최댓값을 Q1, Q3로부터 각각 선으로 연결한다. (* Q1 - 1.5*IQR < min, Q3 + 1.5*IQR > max)
4. 양 경계를 벗어나느 자료값들을 *로 표시하고, 이 점들을 이상점이라고 한다.

상자그림의 장점은 분포의 다양한 특성을 하나의 그림에 함축시키는 것이다. 자료의 중심위치, 퍼진 정도 등의 주어진 수치 이외에도 분포의 대칭성, 분포의 집중정도, 대부분의 자료값들에서 동떨어진 이상관측점 등을 알 수 있다.
도수분포표에서의 자료 요약
자료가 도수분포표로 요약되고 원자료는 주어지지 않을 경우, 각 계급구간의 중간값을 선택하여 그 계급구간의 모든 관측값이 그 값을 갖는 것처럼 평균과 분산 계산이 필요해 보인다. 이때 주의하여야 할 것은 원자료를 그룹화할 경우 그룹화에 의하여 어느 정도의 정보가 상실되기 때문에, 가능하다면 도수분포표보다는 원자료를 통하여 요약치를 계산하는 것이 바람직하다.
도수분포표에서 계급의 개수가 k, 각 계급의 도수가 f_i, 계급구간의 중간값이 m_i, 자료의 개수가 n일 때 평균과 분산은 다음과 같다.

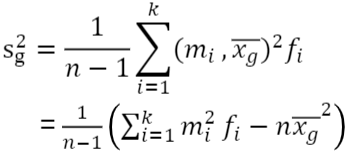
도수분포표로부터 표본평균을 구할 때 각 계급구간의 중간값 m_i가 f_i개 있는 자료처럼 구하였는데 마찬가지로 중앙값과 사분위수, 사분위수범위도 구할 수 있다. 연속형 자료에 있어서 최빈값은 도수분포표를 통하여 얻는다. 즉 도수분포표에서 도수가 가장 많은 계급구간의 중간값이 최빈값이 된다.
한 줄 요약
자료의 객관성, 일관성을 기술적으로 잡기 위해 중심과 퍼짐 정도를 파악해야 한다.
'@ '통계학' 당주힘실' 카테고리의 다른 글
| [당주힘실 통계학] 5. 확률_될 비율 (0) | 2022.08.16 |
|---|---|
| [당주힘실 통계학] 4. 두 변수 자료의 요약 (0) | 2022.08.16 |
| [당주힘실 통계학] 2. 표와 그림_목적에 따라 보기 좋게 (0) | 2022.08.11 |
| [당주힘실 통계학] 1. 서론_모집단, 표본 (0) | 2022.08.11 |
| [당주힘실 통계학] 0. 시작_통계이론사전 (0) | 2022.08.11 |




댓글