당.주.힘.실 : 당신의 주장에 힘을 실어줄
*엑셀편은 microsoft excel 2016을 활용하였습니다
목차
1. 중학교 1학년 남학생 임의 추출 자료
1-1. 신뢰구간 구하기
1-2. 가설검정 보이기
1. 중학교 1학년 남학생 임의 추출 자료
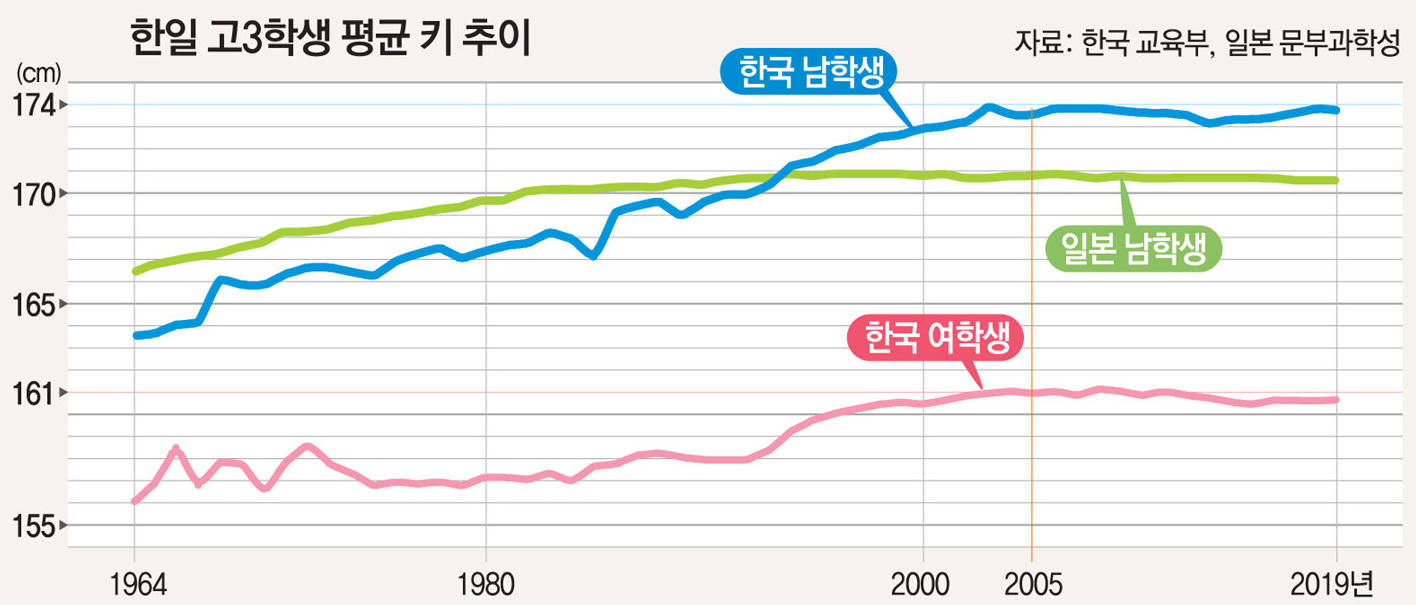
키가 큰 편도 아니었지만 매년 어린 학생들의 평균 키가 점점 커지는 것을 확인할 수 있다. 중학교 1학년의 평균 키는 분산이 매우 클 것이다. 따라서 고3 학생의 평균 키 추이를 보면 본인의 체감은 현실이었음을 증명할 수 있다. 평균 키가 커진 데에는 서구화된 식습관이나 키에 대한 부모의 관심과 투자 등 여러 가지 요인이 있을 것이다. 키에 대한 미련을 버린 지 오래되었지만 점점 좋은 시대에 태어나는 어린 친구들이 참 축복받았다는 생각을 한다. 물론 시대 탓을 하는 것은 아니다. 분산이 매우 큰 중학교 1학년 학생들의 자료를 살펴볼 예정이다.
임의 추출된 28명의 키 자료이며 이를 통해 신뢰구간을 구하고 가설검정을 엑셀로 확인할 예정이다. 이번 해당 자료는 실제 자료는 아니다.
| 120.5 | 164 | 136.6 | 160.6 |
| 119.3 | 158.4 | 142.7 | 173.5 |
| 125.7 | 168.9 | 143.1 | 160.8 |
| 124.5 | 159.7 | 149.2 | 173.5 |
| 131.8 | 171.6 | 150.1 | 160.7 |
| 130.2 | 160.3 | 157.2 | 158 |
| 137.4 | 172.8 | 155.3 | 161 |
1-1. 신뢰구간 구하기
위 주어진 자료에 근거하여 중학교 1학년 남학생의 평균키에 대한 95% 신뢰구간을 구하라.
아래와 같이 자료 입력이 필요하다. 단 하나의 열에만 작성하는 것이 주의 점이다. 별개의 열에 각각 입력하면 기술 통계량 요약 시 각 열에 대한 요약으로 출력될 수 있다.

데이터 탭 - 데이터 분석 - 기술 통계법을 선택하고

요약 통계량의 체크 박스를 선택하여 신뢰수준을 95%로 지정한 후 확인을 누르면 다음과 같이 요약 통계량을 구할 수 있다.


표본의 크기가 28이므로 모집단의 평균에 대한 신뢰구간은 정규분포를 이용하여 근사적으로 구한다. 요약 통계량에 표본 평균, 표준오차, 관측수 등이 주어져 있으므로 엑셀에서 함수 CONFIDENCE.NORM(alpha, standard_dev, size) 를 이용해서 구하면 된다. 결과를 보면 표준편차 셀과 관측수가 주어져 있는 셀 자체를 활용하여 구한다.
이 결과를 이용하여 아래 그림에서와 같이 셀에 위 함수를 입력하여 구할 수 있다. 그 값은 6.260389 임을 알 수 있다.

여기서 한 가지 주의할 점은 신뢰 수준이라고 하는 부분에 이전에 소개한 신뢰 수준과 의미가 전혀 다르다는 점이다. 엑셀에서는 신뢰수준을 신뢰구간을 구할 때 추정치로부터 가감되는 양을 일컫는다. 이와 같은 예는 기술 통계법의 결과 가장 밑에 주어져 있는 신뢰 수준에서도 찾을 수 있는데, 이것은 다음 장에서 다룰 내용으로 모집단이 정규분포를 따를 때 적용하는 t 분포를 이용한 신뢰구간에서 계산된 값이다. 이와 같이 엑셀에서의 신뢰수준의신뢰 수준의 의미는 엑셀에서만 통용되는 것으로 본래의 신뢰 수준의 의미와는 많이 다르다는 사실을 기억해야 한다.
1-2. 가설검정 보이기
만약 위에 추출된 28명의 중학생 1학년의 남학생 키가 A도시에서만 추출되었다면 다른 B도시에서의 중학교 1학년 남학생의 평균 키가 155cm와 차이가 있다고 할 수 있는지 판단이 필요할 것이다. 이러한 경우 검정하고자 하는 가설은 아래 두 가지로 볼 수 있다.
1. 평균 = 155
2. 평균 ≠ 155
가설을 검정하기 위한 검정통계량의 값을 구하기 위하여 먼저 기술 통계법을 이용해 요약 통계량을 구한다. 이는 1-1을 참고한다.
각각의 통계량 값이 주어져 있는 위치를 지정하여 아래와 같이 지정한 셀에 입력하면 그 값을 구할 수 있다. 위의 대립 가설로부터 양측 검정에 대한 P-값은 2*P 이므로 다음과 같이 구할 수 있다.



통계량 Z값은 일반 수식에 의해서 -1.259로 확인되었고, B도시 추정 평균키 155cm에 대한 양측 검정 p-값은 NORMSDIST와 ABS를 사용하여 이 또한 일반 수식으로 0.208 수준으로 확인했다.
결론은 P-값이 0.208로 상당히 커서 귀무가설을 기각할 수 없으므로, 중학교 1학년 남학생의 평균 키가 155와 차이가 난다고 판단할 수 없다. 이전과 유사하듯 이론적인 계산값과 비교하게 되면 그 값에 대한 오차는 있을 수 있으나 판정에 대한 결과는 같다.
'@ '통계학' 당주힘실' 카테고리의 다른 글
| [당주힘실 통계학_엑셀편] 22. 수질 지표로 t분포에서 신뢰구간과 가설검정, 정규성 가정에 대한 적합성 확인 (0) | 2022.09.27 |
|---|---|
| [당주힘실 통계학_엑셀편] 20. 추출된 표본인 로또 번호의 역대 분포로 평균내고 히스토그램 그리기 (1) | 2022.09.16 |
| [당주힘실 통계학_엑셀편] 19. 전력소비 행태의 정규분포를 통한 자료 분석 (0) | 2022.09.16 |
| [당주힘실 통계학_엑셀편] 18. 고속도로 교통량을 통한 예측(이항분포, 포아송분포 확인하기) (0) | 2022.09.09 |
| [당주힘실 통계학_엑셀편] 17. 폭우관련 역대 강수량 자료를 요약한다(평균, 분산 등 & 관계) (1) | 2022.09.07 |




댓글