당.주.힘.실 : 당신의 주장에 힘을 실어줄
*엑셀편은 microsoft excel 2016을 활용하였습니다
목차
1. 산업별 전력소비 행태
1-1. 평균과 분산
1-2. 정규분포를 따를 때 질문(2)
2. 정규분포에서의 엑셀 활용
2-1. 엑셀을 통한 정규분포에서 답 구하기
2-2. 정규확률그림 그리기
1. 산업별 전력소비 행태
대한민국은 친환경을 목표로 디지털 중심의 전력 ICT 플랫폼을 확장 중이다. 빅데이터를 사용하여 시간별, 주택과 산업별로 소비행태를 분석하고 그에 맞게 송변전의 효율을 향상한다. 에너지 절약은 물론 저장된 에너지를 필요한 곳에 다시 팔 수도 있는 세상을 구현 중이다. 여기에 산업별 전력소비 행태를 찾아보았다.
자료는 KOSIS 출처, 2021년 각 월마다 1시 기준 산업별 전력소비이다. (* 사진 속 링크 참고)
자료의 제시된 바로는 전력소비자의 시간별 소비량 데이터를 바탕으로 가공된 상대 계수이다. 일간 평균을 기준(=1,000)으로 하여 사용량을 상대적으로 산출된 것이다.


1-1. 평균과 분산
대한민국 전체 산업군의 전력소비가 조사되었다. 이 모든 자료를 표본으로 하여 2021년 산업군에 소비된 전력의 평균과 분산을 조사한다. 지난 장에 있던 엑셀을 이용하여 평균과 분산을 간단히 구할 수 있다.
평균 : =AVERAGE(범위)
(표본)분산 : =VAR.S(범위)

위와 같이 평균은 754, 분산은 28196.7485 임을 알 수 있다. 계수의 일간 평균을 1000으로 고정한 것을 감안하면 상대적으로 전력을 소비하지 않는 산업군이 있으며 그 편차가 비교적 크다는 것을 알 수 있다.
1-2. 정규분포 가정하여 질문에 답하기
산업군 별로 월마다 전력소비 계수를 평균 내었다. 정규분포를 따른다고 가정하여 아래 두 가지 질문을 수학적으로 계산한다. 이후 2절에서 엑셀을 이용하여 구하고 비교할 예정이다.

(1) 전력소비 계수가 500 이하의 산업군은 몇 퍼센트나 되겠는가
확률변수 X를 전력소비 계수라고 하면 아래와 같이 구할 수 있다.




정답 : 6.552%
(2) 상위 10% 산업군에 A를 준다고 하면 몇 점 이상이 되어야 A를 받을 수 있겠는가
x점 이상의 산업군에게 A를 준다고 하면 x는 다음을 만족시켜야 한다.


z 값은 표준정규분포표로부터 찾고, 가운데 값으로 내분점을 향해도 되지만 그렇지 않을 때에는 가까운 값으로 고르면 된다. 그러면

정답 :969점 이상이 A를 받음
전력을 많이 소비하는 산업은 어업, 석유정제품 제조업, 1차 금속 제조업, 의료/정밀/광학기기 및 시계 제조업, 전기/가스/증기 및 공기조절 공급업, 하수/폐수 및 분뇨 처리업이 있겠다. 간단히 이러한 트렌드를 알아보았다.

2. 정규분포에서의 엑셀 활용
2-1. 엑셀을 통한 정규분포에서의 답 구하기
함수 NORM.DIST는 정규분포에서의 확률을 구하는 경우, 함수 NORM.INV는 정규분포의 역함수 값을 구하는 경우에 사용한다. 아래의 구문에서 보면 분산 대신 표준편차가 입력되는 점에 유의하여야 한다.
NORM.DIST(x, mean, standard_dev, cumulative) : x이하의 확률
NORM.INV(a, mean, standard_dev) : 아래에서 a의 확률에 해당하는 경곗값
X : 확률분포를 구하려는 변량의 값
Mean : 확률분포의 산술평균
Standard_dev : 확률분포의 표준편차
Cumulative 함수의 형태를 결정하는 논리값으로서 TRUE이면 NORM.DIST는 누적분포함수를 FALSE이면 확률밀도함수를 제공한다.
1-2에서 확인하려 했던 질문과 엑셀을 통한 값을 비교해보자. 원하는 수를 조건에 따라 입력하면 된다. 입력한 것은 빨간 박스를 참고한다.
(1) 전력소비 계수가 500 이하의 산업군은 몇 퍼센트나 되겠는가
정답 : 6.552%

6.5187% 값을 확인할 수 있다. 계산값과 0.5% 차이를 보인다.
(2) 상위 10% 산업군에 A를 준다고 하면 몇 점 이상이 되어야 A를 받을 수 있겠는가
정답 :969점 이상이 A를 받음

969.1981 값을 확인할 수 있다. 계산 값과 0.02% 차이를 보인다.
상위 10%에 해당하는 값은 아래에서부터 90%에 해당하는 값이므로 셀 첫 번째 항목에 0.9로 설정하였다.
2-2. 정규확률그림 그리기
자료를 오름차순으로 정렬한 후 i번째 자료의 정규 점수는 확률 i/(76+1)인 표준 정규분포의 역함수 값이므로 엑셀의 함수 NORMS.S.INV를 이용하여 구한다. 다음의 단계를 거쳐 정규확률그림을 그릴 수 있다. 각 열의 이름을 다음과 같이 정하고 엑셀 작업을 한다.

1. 순위 셀에 =RANK(O3,O3:O76,1) 을 입력한다.
2. 아래 그림의 점 버튼을 더블클릭하여 순위 칸을 모두 채운다.

3. 자료가 76개이므로 i번째 자료의 정규 점수는 표준 정규분포에서 확률 i/(76+1)에 해당하는 역함수 값이므로 정규 점수 셀에 =NORM.S.INV(P3/77)을 입력하고 순서2와 같이 자동 채우기를 한다.
4. 자료의 값을 x축, 정규점수를 y축으로 하여 분산형을 그려본다. 임의의 점을 선택하고 마우스 오른쪽 버튼을 클릭하여 데이터 계열 서식 - 채우기 및 선 - 그래프 표식 - 표식 옵션에서 기본 제공의 형식을 바꾸고 크기를 5로 설정했다.
또한 x축을 마우스 오른쪽 클릭하여 축서식 - 축옵션에서 x축의 최솟값을 380으로 지정하였다. 만약 그림 안쪽에 x축이 그려지면 y축을 마우스 오른쪽 버튼으로 클릭하여 축서식에서 세로축 교차의 축 값을 y축의 최솟값으로 지정하여 주면 된다.
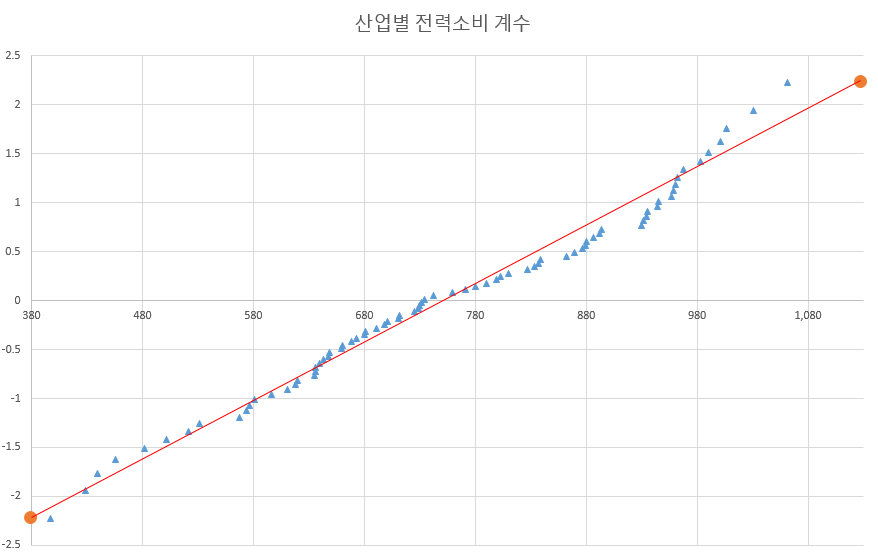
5. 자료의 정규성을 판단하기 위해서는 자료와 똑같은 평균과 표준편차를 갖는 정규분포로ㅜ터 이상적인 표본을 추출한다고 할 때 그 표본의 정규확률그림과 위의 그림을 비교해 보는 것이 필요하다.
여기에서 말하는 이상적인 표본이란 앞의 본문에서 설명한 바 n개의 관측치가 분포를 등확률로 나누는 경계점들로 이루어진 표본을 말한다. 이때의 정규확률그림은 정규 점수에 대하여 이상적인 관측값이 다시 정규 점수라는 관계식으로부터 직선이 되는 것을 알 수 있다. 이 직선과 위 그림을 비교하면 자료의 정규성을 어느 정도 판단할 수 있다.
직선은 (-2.226599895*표준편차+평균,-2.226599895) ~ (2.226599895*표준편차+평균,2.226599895)을 잇는다.


최종적으로 아래와 같이 그래프를 그릴 수 있고 직선과 함께 자료의 정규성을 파악할 수 있었다.
'@ '통계학' 당주힘실' 카테고리의 다른 글
| [당주힘실 통계학_엑셀편] 21. 중학교 1학년 남학생 30명 키를 통한 신뢰구간과 가설검정 확인하기 (0) | 2022.09.27 |
|---|---|
| [당주힘실 통계학_엑셀편] 20. 추출된 표본인 로또 번호의 역대 분포로 평균내고 히스토그램 그리기 (1) | 2022.09.16 |
| [당주힘실 통계학_엑셀편] 18. 고속도로 교통량을 통한 예측(이항분포, 포아송분포 확인하기) (0) | 2022.09.09 |
| [당주힘실 통계학_엑셀편] 17. 폭우관련 역대 강수량 자료를 요약한다(평균, 분산 등 & 관계) (1) | 2022.09.07 |
| [당주힘실 통계학_엑셀편] 16. 출산국가 자료로 히스토그램, 파레토 그려보기 (0) | 2022.09.06 |




댓글